Background

The short story (tl;dr)

Many processes of diversification can cause simultaneous (and potentially multifurcating) divergences, but current phylogenetic methods for inferring rooted trees assume evolutionary lineages diverge independently (and only bifurcate). This leaves us without a good way to infer the patterns of shared divergences predicted by these processes. To solve this problem, we generalized the space of topologies considered during phylogenetic inference to include trees with shared or multifurcating divergences. This allows us to jointly infer relationships, divergence times, shared divergences, and multifurcating divergences, and test for patterns of divergences predicted by processes of diversification that simultaneously affect multiple lineages.

The longer story

Many processes of diversification can simultaneously affect multiple lineages. For example, below is an animation of three species of lizards co-occurring on an island that is fragmented twice by rising sea levels.

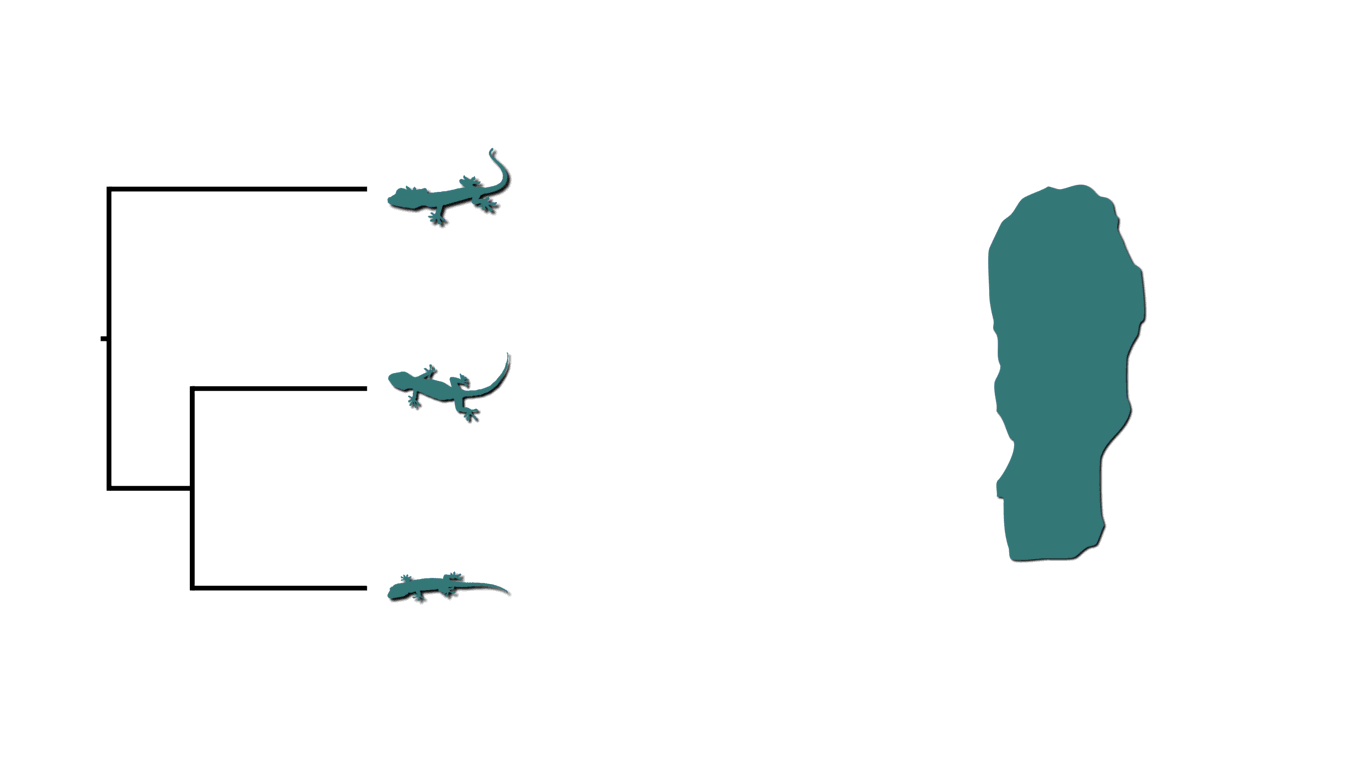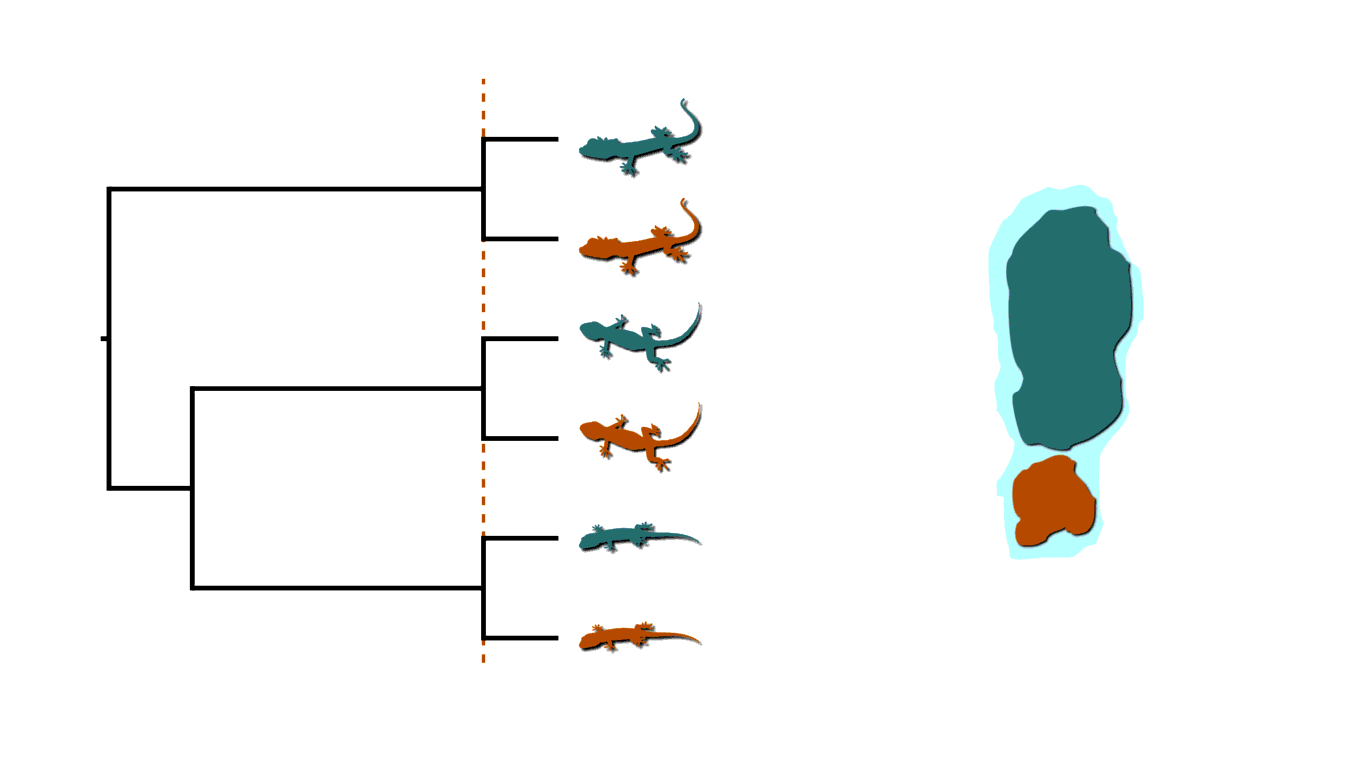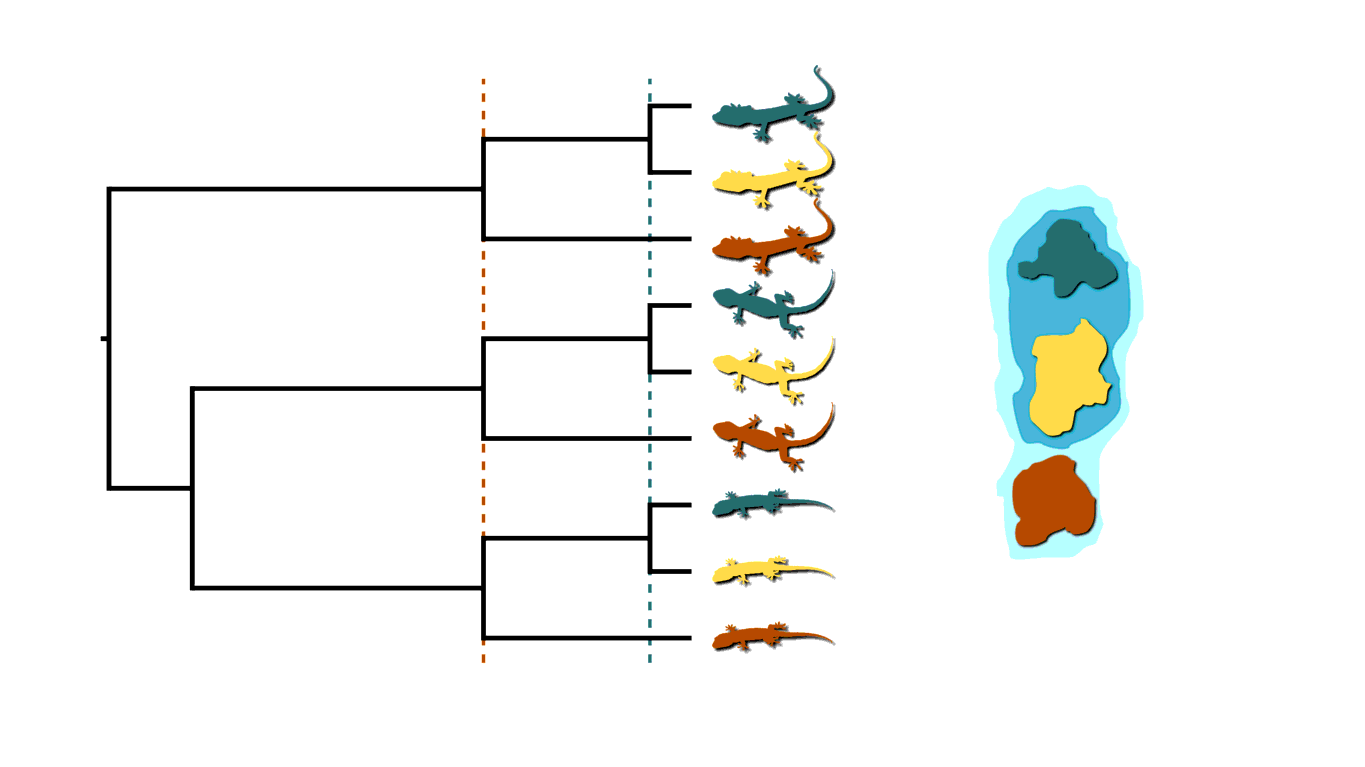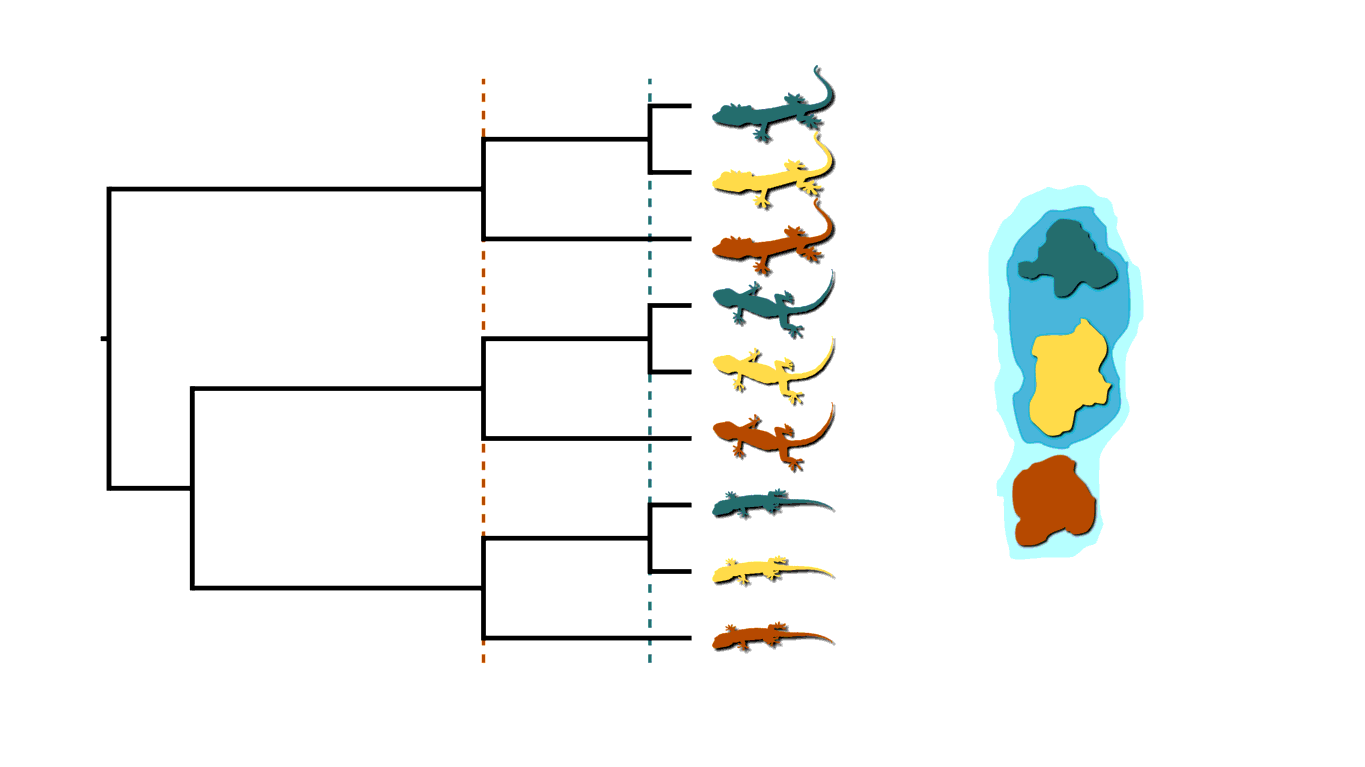
Island fragmentation causing shared divergences.

This creates two bouts of shared divergences across the tree, indicated by the dashed lines above. In addition to biogeography, there are many other examples of processes of diversification that generate patterns of shared divergences. Instead of lizards on islands, let’s imagine three members of a gene family residing along a region of a chromosome that gets duplicated. This would create shared divergences across the phylogenetic history of the gene family. In epidemiology, when multiple infected individuals spread the pathogen to others at a social gathering, this will create shared divergences in the “transmission tree” of the pathogen.

If rising sea levels fragments the island into more than two island, like in the animation below, this will not only cause shared divergences among lineages, but also multifurcations (a lineage diverging into three or more descendants).

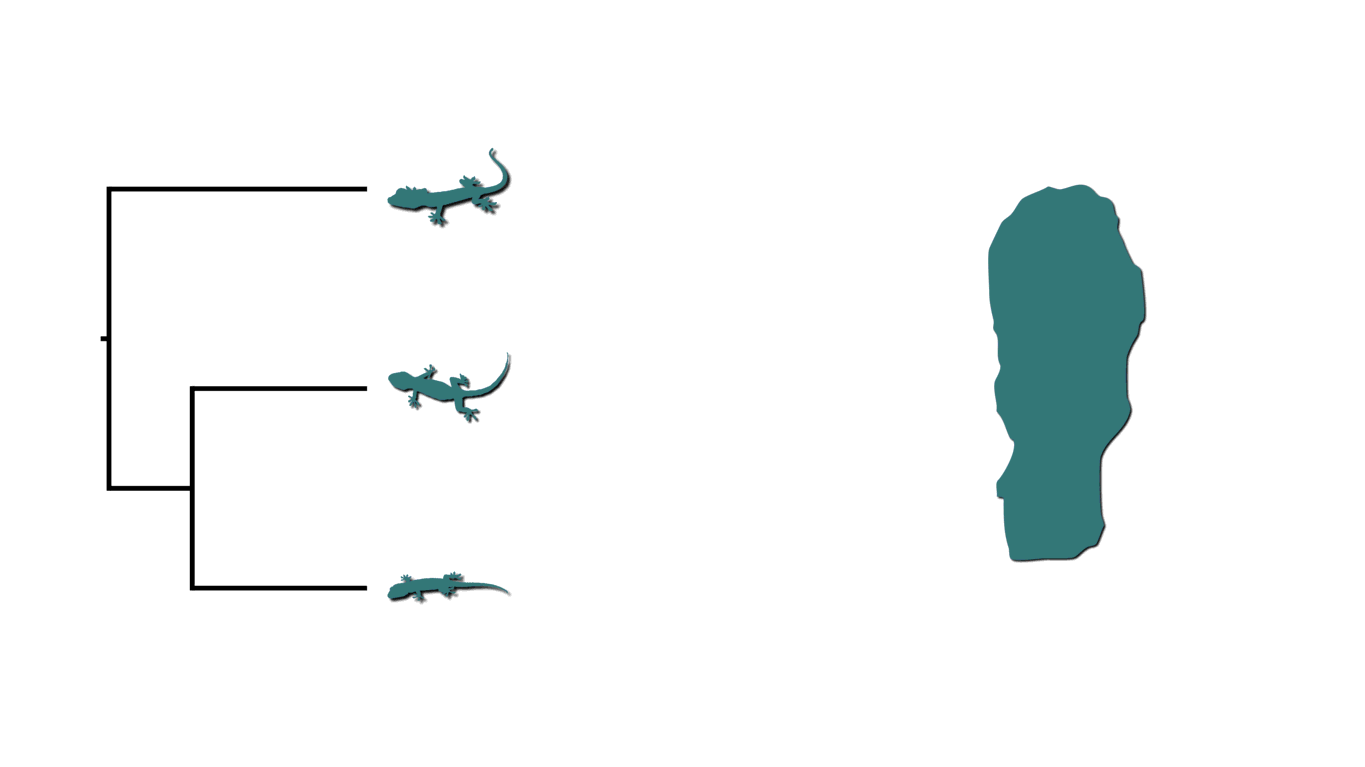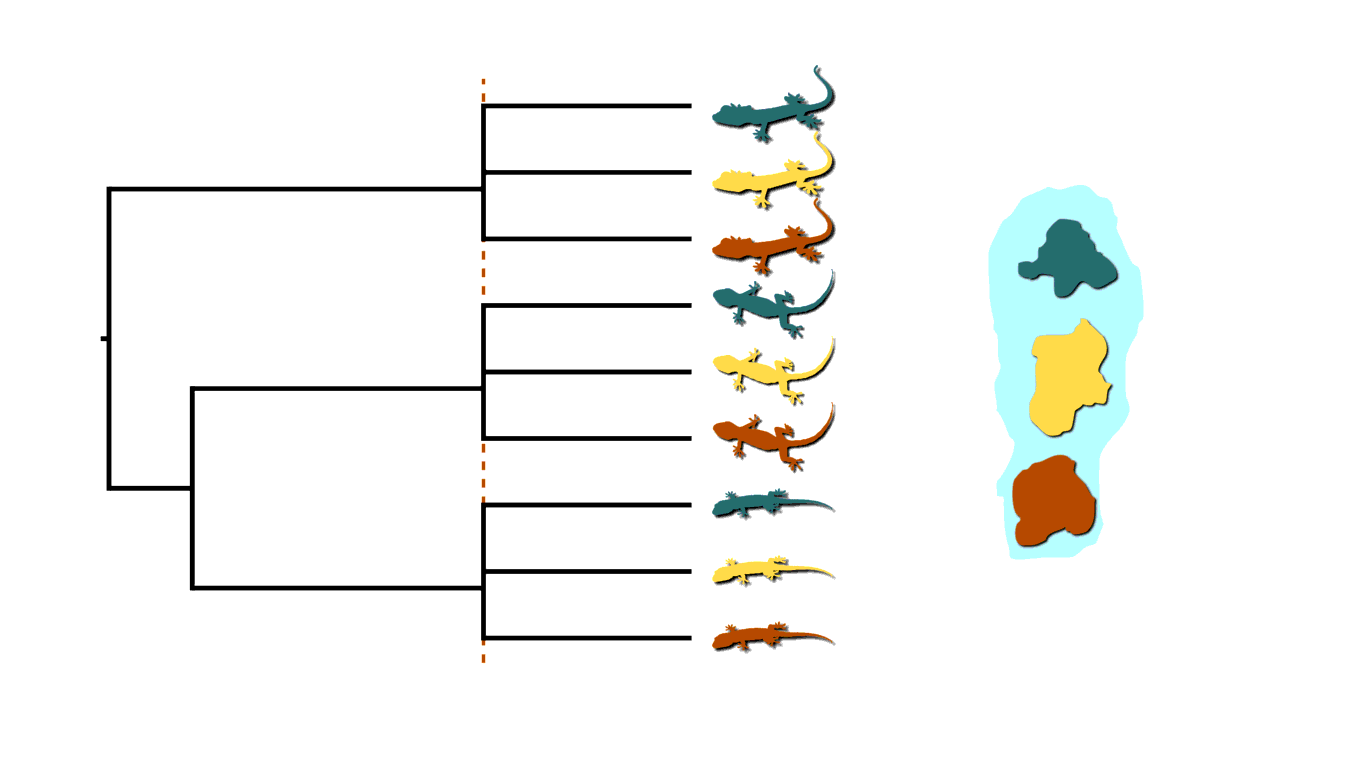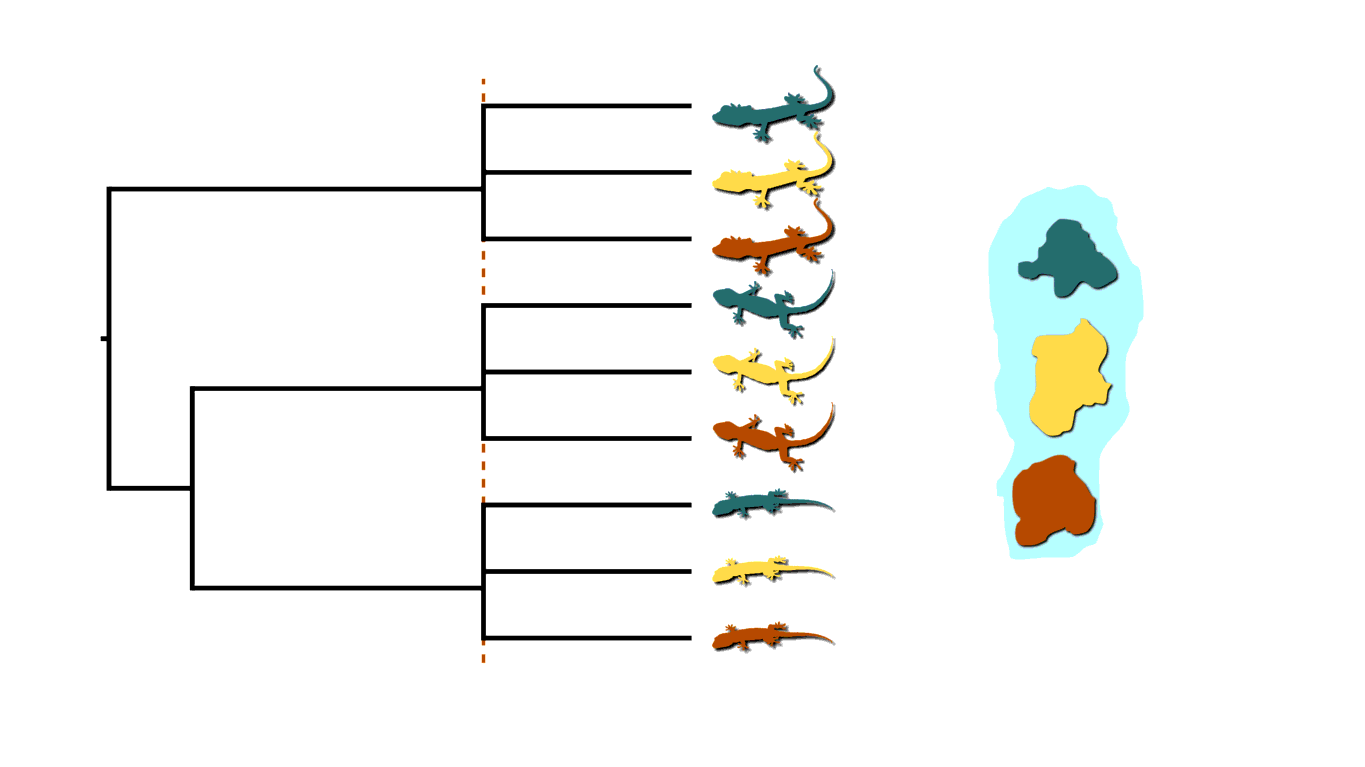
Island fragmentation causing multifurcating, shared divergences.

Similarly, when an infected individual spreads a pathogen to two or more others at a social gathering, this will create a multifurcating divergence in the transmission tree.

Current phylogenetic methods for inferring rooted trees assume all divergences are independent and bifurcating. In other words, if we have tips, current methods only consider trees with independent, bifurcating divergences. When shared and/or multifurcating divergences were common in the system we want to study, such tree models are over-parameterized as illustrated in the figure below. More importantly, by assuming all divergences are independent and bifurcating, current phylogenetic methods do not allow us to test for patterns of shared or multifurcating divergences predicted by processes of diversification that are of interest across the life sciences.

When shared or multifurcating divergences have occurred, current phylogenetic models are over-parameterized.

To relax the assumption of independent, bifurcating divergences, phycoeval uses a Bayesian approach to generalizing the space of tree models to allow for shared and multifurcating divergences [20]. Under the generalized tree model implemented in phycoeval, trees with bifurcating divergences are only one class of tree models in a greater space of trees with anywhere from potentially shared or multifurcating divergences.

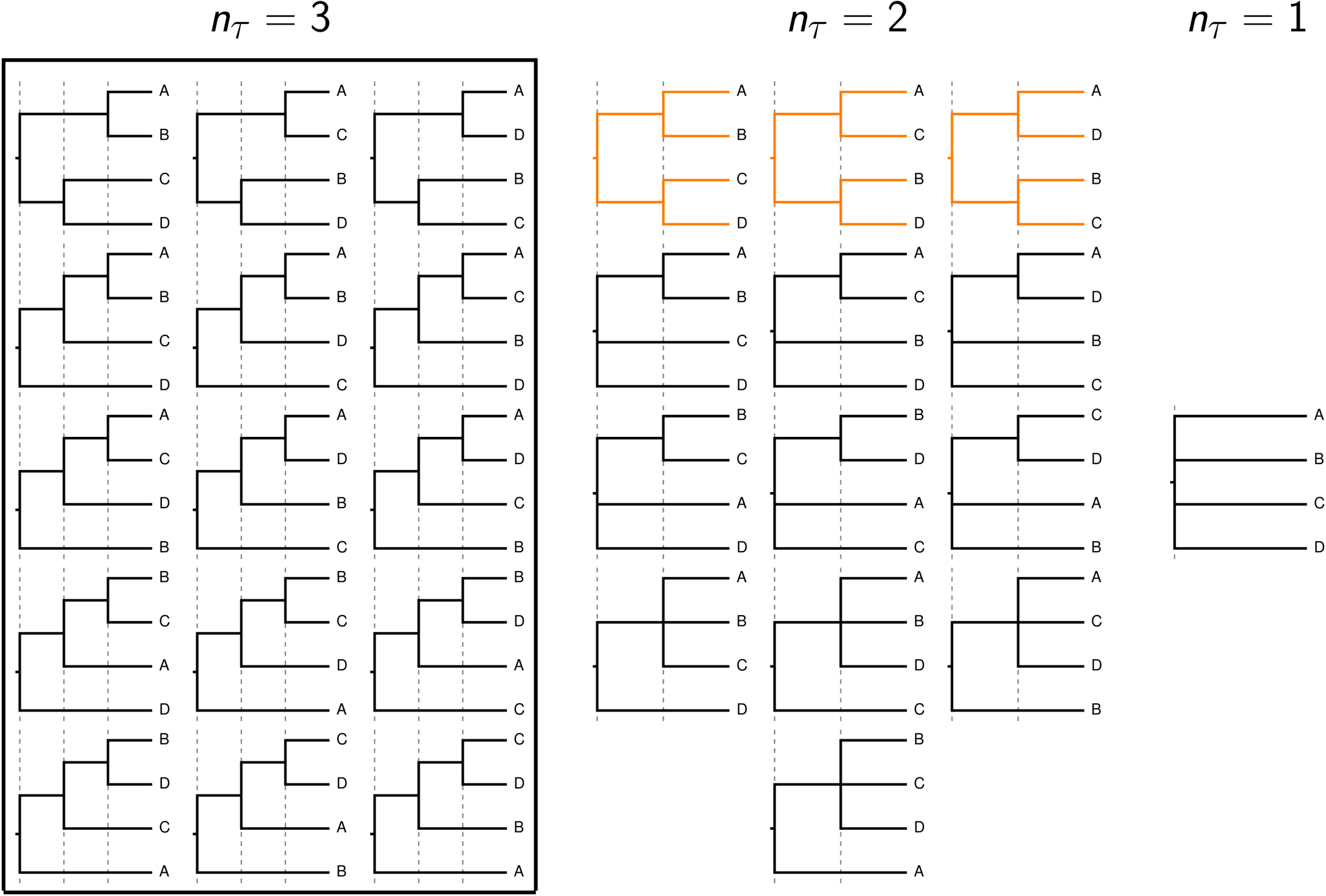
The rooted topologies considered by current phylogenetic methods (within box) and the additional tree models considered by phycoeval’s generalized tree model. The tree models with nonindependent (shared) divergences are highlighted in orange.

Phycoeval uses reversible-jump Markov chain Monte Carlo algorithms to sample this generalized space of trees. This allows joint inference of relationships, shared and multifurcating divergences, and divergence times.

In phycoeval, we coupled the generalized tree model with the “SNAPP likelihood” for directly calculating the probability of biallelic characters given a population (or species) phylogeny, while analytically integrating over all possible gene trees under a coalescent model and all possible mutational histories along those gene trees under a finite-sites model of character evolution [3][14]. This allows us to jointly infer a species tree and shared divergences from genomic data [20].